Ci vorrebbero più di 100 mila anni per elaborare, a mano, una previsione meteo a 3 giorni

Necessari circa 1500 mila miliardi di operazioni per una previsione credibile a 3 giorni, su un box di 8 km di lato.
di Mario Giuliacci
www.meteogiuliacci.it

Le leggi  fisiche dell’atmosfera espresse da equazioni note ma troppo difficili da risolvere 

Le leggi che descrivono l’evoluzione dell’atmosfera sono quelle classiche della meccanica e della termodinamica, e la loro generale formulazione è nota da più di due secoli.

Purtroppo, però,  a causa della complessità medesima dei fenomeni atmosferici, sono leggi molto complesse, ed espresse pertanto da equazioni di difficile risoluzione.

Questo è il motivo per cui, per l’impostazione rigorosamente scientifica del problema delle previsioni meteorologiche, si è dovuto attendere gli anni ’70, quando la potenza di calcolo raggiunta dai computer ha permesso la risoluzione diretta, seppure approssimata, del sistema di equazioni nel volgere di qualche ora, simulando e schematizzando il comportamento dell’atmosfera attraverso appropriati modelli fisico-matematici.

Le condizioni dell’atmosfera a un dato istante e la sua evoluzione negli istanti successivi possono teoricamente essere conosciute con esattezza qualora siano noto, punto per punto, il valore osservato o detto assunto da circa 200 variabili che ne definiscono lo stato iniziale (temperatura, umidità, pressione, vento su 50-100 livelli)

Quindi si tratta, in pratica, di risolvere il sistema  di circa 200 equazioni che legano tra di loro circa le 200 variabili “predettande”

Cosa è un modello fisico-matematico

L’insieme dei metodi e delle approssimazioni, fisiche e matematiche, impiegate per risolvere tale sistema di 200 equazioni in 2000 incognite, costituisce il modello fisico-matematico.

Tali equazioni sono differenziali, ossia vi compaiono le derivate spaziali  e temporali delle variabili incognite, ossia la rapidità di variazione nel tempo e nello spazio delle prescelte variabili.

Molti dei processi fisici sono ancora mal conosciuti, e pertanto nelle equazioni vengono approssimati (in gergo “parametrizzati”) con relazioni semi-empiriche, come nei processi di scambio di calore  e vapore tra il suolo  e l’aria sovrastante.

Per altri processi, la legge è rigorosamente nota (ed esempio, la legge di Stephan-Boltzmann, che esprime la quantità di radiazione infrarossa emessa in un secondo da 1 metro quadrato di un corpo che abbia una data temperatura)  ma spesso i termini da aggiungere nelle equazioni sono così complicati da consigliare consistenti semplificazioni.

Da quanto fin qui detto si arguisce che l’evoluzione dell’atmosfera è, nella pratica, descritta da equazioni precedentemente sottoposte a svariate approssimazioni fisiche.

Sfortunatamente, le equazioni dell’atmosfera sono complesse da non ammettere soluzioni analitiche note

Una matematica ad hoc anche se fonte di errore per risolvere le complesse equazioni

L’unica alternativa possibile per la risoluzione del sistema di equazioni è quella di far ricorso ai metodi proposti dall’analisi numerica, una branca della matematica che insegna i metodi per esprimere le derivate come semplici operazioni algebriche tra “numeri”. La tecnica numerica richiede una mole impressionante di operazioni, e pertanto la soluzione del sistema di equazioni in 200 incognite circa, può essere ricavata in tempi accettabili soltanto con l’ausilio di potenti elaboratori.

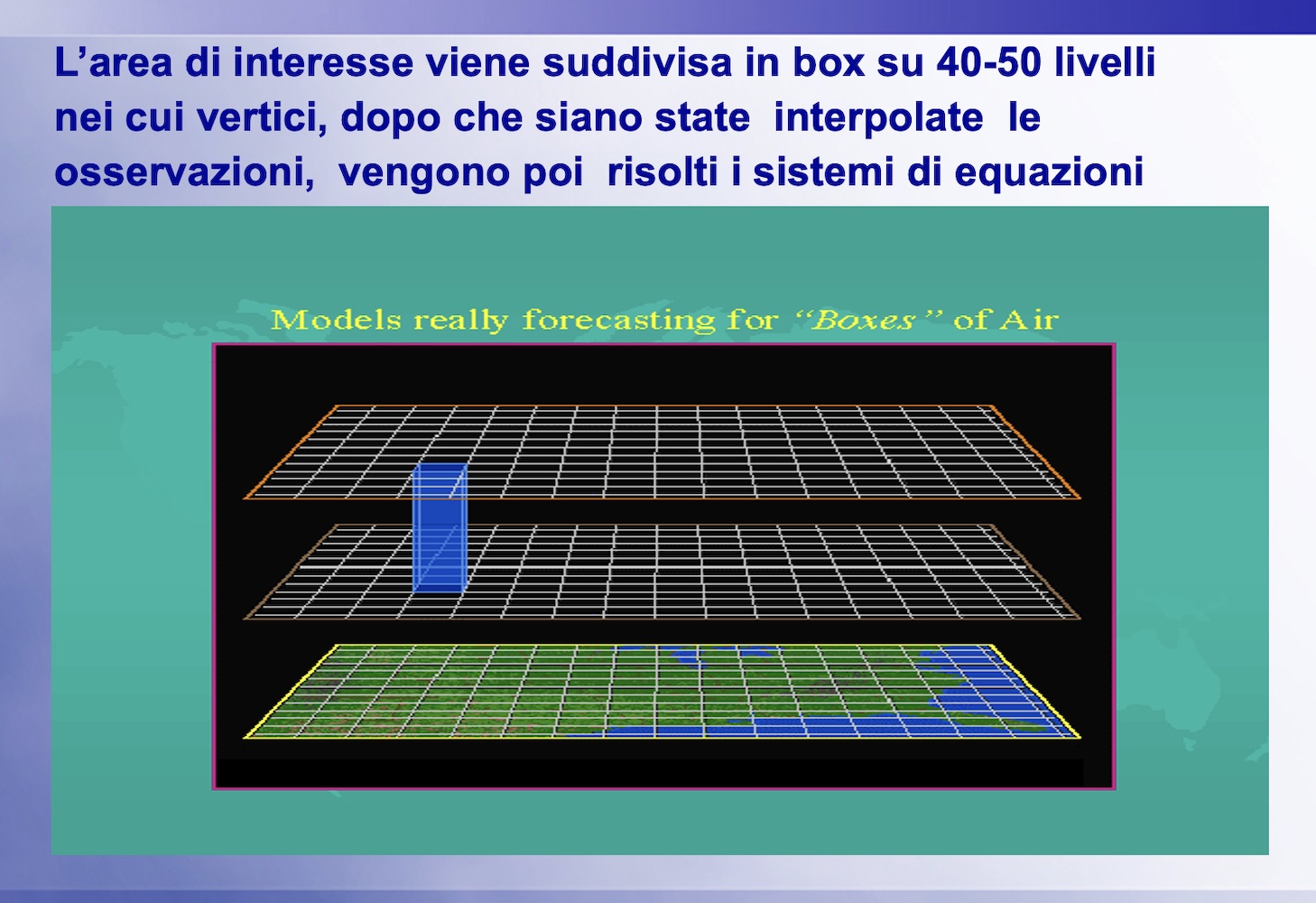
Per l’applicazione del metodo numerico si suppone, innanzitutto, che lo stato e l’evoluzione del tempo sulla regione oggetto della previsione possano essere adeguatamente rappresentati mediante i valori assunti, con il passare del tempo t dalle 200 variabili predittande in un numero finito di punti, opportunamente spaziati sia nel piano orizzontale che verticale, e ottenuti dalla suddivisione dell’atmosfera in un grigliato di box.

I tanti step in un modello fisico-matematico per arrivare alla previsione

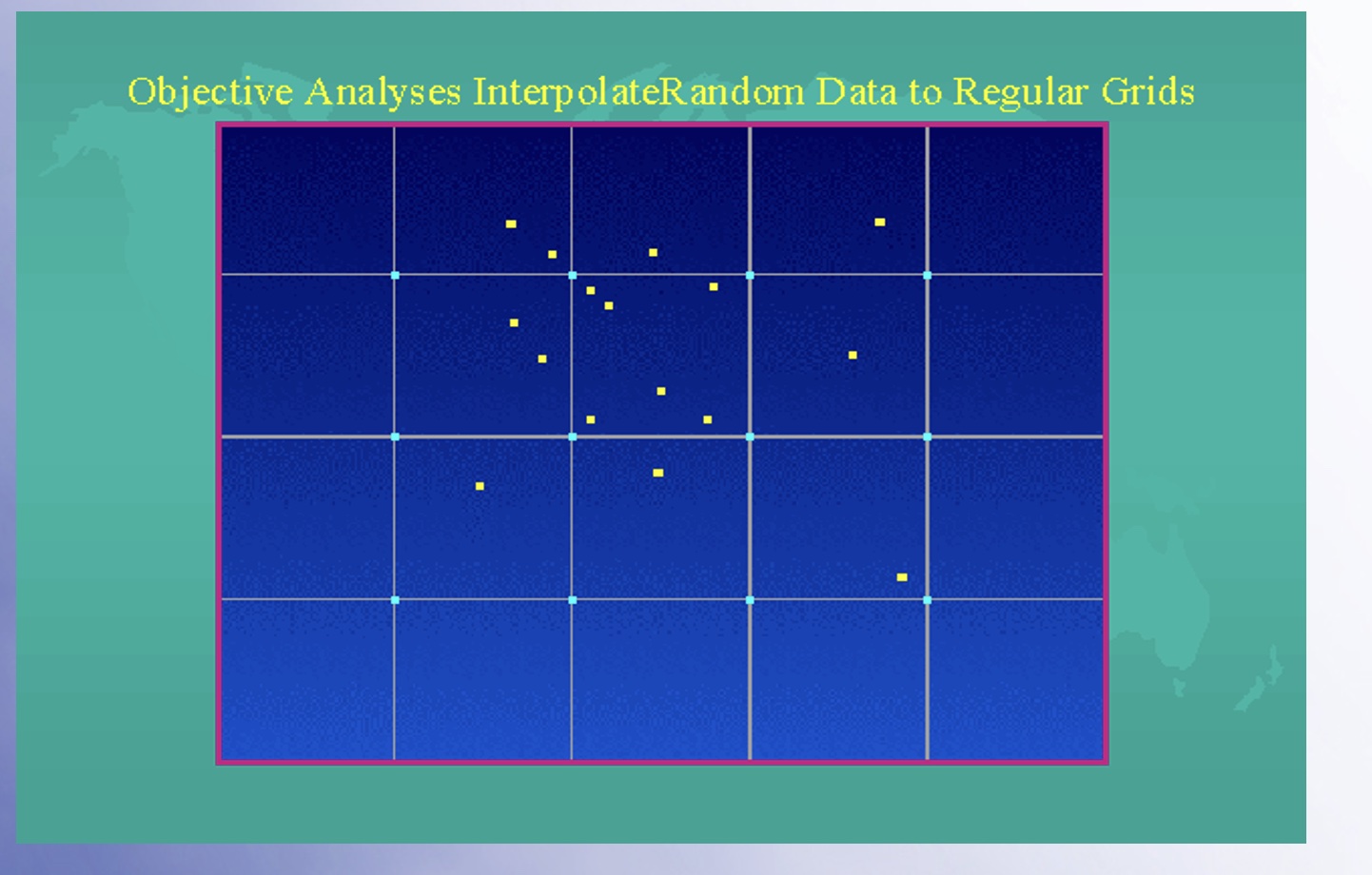
La interpolazione

La risoluzione dell’enorme numero di sistemi di equazioni ha inizio una volta che in tutti i “nodi”  ( i vertici dei box di quadrati in cui è stta suddivisal’èare adi interesse) siano stati assegnati i valori iniziali delle 200 variabili, come ottenuti dalle osservazioni sinottiche.Siccome la posizione delle osservazioni ovviamente non coincide con quella dei nodi di griglia, si rende necessaria un’operazione preliminare di “interpolazione” dei dati di osservazione nei punti di griglia.

Tale operazione introduce naturalmente degli errori nella descrizione dello stato iniziale dell’atmosfera, e questi sono tanto più consistenti quanto più l’area è povera di informazioni. Là dove non vi sono poche  osservazioni ( es. mari , oceani), al posto dell’osservazione si introduce il valore della variabile prevista dal modello 6 ore prima.

L’elaboratore, dopo aver completato l’interpolazione, si avventura nella risoluzione numerica del complesso sistema di equazioni.

La risoluzione delle equazioni “iterata” ogni 10 secondi circa

Le equazioni consentono di ricavare, tramite le derivate temporali che figurano a primo membro  (esempio nelle equazioni del moto  a primo membro compare l’accelerazione del vento V ovvero DV/Dt ) l’incremento o decremento che le singole variabili subiranno nello step temporale Δt successivo allo stato iniziale.

L’operazione, effettuata per tutti i nodi e per tutte le 200 variabili predittande, consente di prevedere quale sarà lo stato in cui verrà a trovarsi l’atmosfera Δt secondi dopo l’istante iniziale. Il procedimento viene “iterato” un numero di volte pari a quello necessario per coprire il periodo di validità della previsione.

Senza PC occorrerebbero  più di 100 mila anni per un previsione a 3 gg. Un esempio pratico

Per una previsione di 3 giorni un’area dii 2000×2000 km2 che abbracci tutta l’Italia, su ogni pixel di 8 km di lato e su 40 livelli verticali (come negli attuali modelli WRF), con uno step temporale di 15  secondi, il numero di operazioni richiesto al computer per una previsione a 72 ore è, grosso modo, di 1500 mila miliardi di operazioni!

Per eseguire una mole così impressionante di calcoli, un milione di valenti matematici, impiegati 24 ore su 24, e in grado di eseguire un’operazione ogni 5 secondi, fornirebbero il responso dopo circa  100 mila anni! Previsione …in Ritardo!

All’ultimo passo temporale finalmente, in ogni nodo i valori previsti, MA APPROSSIMATI, di vento, temperatura, pressione e umidità

La previsione di tali grandezze, pur essendo scaturita da equazioni inizialmente assai rigorose, risulta in realtà imprecisa, in parte a causa delle numerose approssimazioni fisiche e matematiche introdotte per risolvere le equazioni stesse e, in parte, per l’indeterminazione delle condizioni iniziali derivate dalle osservazioni. 

Ma se, CON UN AIPOETSI DI..4^ grado, i fenomeni fisici fossero perfettamente conosciuti, se le osservazioni iniziali fossero complete e, ancora, se si avesse a disposizione una potenza di calcolo illimitata, sarebbe possibile effettuare previsioni perfette per un qualsivoglia intervallo di tempo? La risposta è, purtroppo no. Una caratteristica nota come effetto farfalla.

Fonte Articolo: Col. Mario Giuliacci